5.Medida de la información

Versión audible de la actividad:

La información, al igual que ocurre con el peso o con el volumen, se puede medir. Dependiendo de si tenemos más o menos cantidad de información usaremos unas u otras de las siguientes unidades de medida:

• bit (b): Es la unidad más pequeña de información. La palabra bit proviene de Binary digIT , es decir dígito binario en castellano.Los únicos valores de información que puede contener son 0 y 1.Como vimos en la sección anterior un bit de información almacenado por ejemplo en la memoria RAM equivaldría a un transistor con voltaje bajo si tiene almacenado un 0 o con voltaje normal si tiene almacenado un 1:

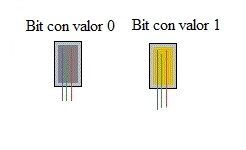
Gráfico de dos bits de memoria con valores 0 y 1 (Fuente:Elaboración propia)

Un bit en un disco duro equivaldría a cada zona de su superficie con cargas magnéticas:

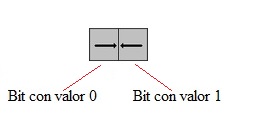
Gráfico de dos bits de disco duro con diferentes valores (Fuente: Elaboración propia)

En un DVD equivaldría a cada zona de su superficie donde hay un valle (cero) o una cumbre (uno):

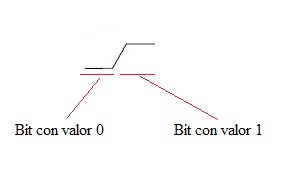
Gráfico de dos bits con valores cero y uno en la superficie de un DVD (Fuente: Elaboración propia)

 

• Byte (B):Equivale a 8 bits, y es la cantidad necesaria de bits para almacenar un carácter. Por ejemplo un archivo de texto con 10 caracteres, ocuparía en memoria 10 bytes o lo que es lo mismo 80 bits.

1 B = 8 bits

• Kilobyte (KB):Un Kilobyte es igual a 1024 Bytes. Esta unidad de medida se usa para expresar la cantidades pequeñas de información.

1 KB=1024 Bytes= 2¹⁰ Bytes

• Megabyte(MB):Un Megabytes es igual a 1024 Kilobytes. Se usa para cantidades medianamente grandes de información, por ejemplo para expresar lo que ocupa un archivo de música.

1 MB= 1024 KB=  2²⁰ Bytes

• Gigabyte (GB): Un Gigabye son 1024 Megabytes. Esta unidad se usa para cantidades grandes de información como por ejemplo para expresar la capacidad de un disco duro.

1 GB= 1024 MB= 2³⁰ Bytes

• Terabyte (TB): El Terabyte equivale a 1024 GB. Se utiliza para cantidades enormes de información como para medir la capacidad de almacenamiento de una supercomputadora o de algunos discos duros actuales.

1 TB= 1024 GB= 2⁴⁰ Bytes

 En el siguiente esquema vemos un resumen en forma de escalera de cómo hacer las conversiones entre las diferentes unidades de medida de la información, para pasar de una unidad más grande a otra más pequeña,es decir bajar escalones, multiplicaremos y para pasar de una más pequeña a otra mayor, es decir subir escalones, dividiremos:

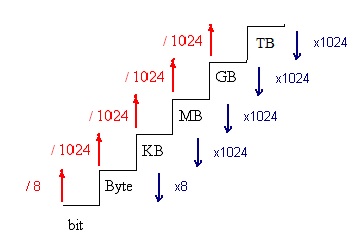
Escalera de conversión entre las diferentes unidades de medida de la información (Fuente: Elaboración propia)

 

Veamos como utilizar las unidades que acabamos de explicar en dos tipos de problemas que se nos pueden presentar en la vida real:

Problema tipo 1:

Hemos descargado de Internet una película que ocupa 3,7 GB. Deseamos grabarle a un amigo dicha película utilizando CD´s, que tienen una capacidad de 700 MB cada uno. ¿Cuantos CD´s necesitaremos?

Para resolver el problema debemos tener la misma unidad de medida tanto en el tamaño que ocupa la película como en la capacidad que tienen los soportes donde queremos grabarla. Para evitar tener que trabajar con cantidades de muchos decimales lo más fácil será pasar de la unidad de medida más grande a la más pequeña multiplicando, es decir convertir el tamaño que ocupa la película de GB a MB, según la escalera de conversión para pasar del peldaño de GB al peldaño de MB debemos de multiplicar por 1024 la cantidad:

3,7 GB= 3,7 x 1024 = 3788,8 MB

Ya tenemos el tamaño de la película en MB, ahora sólo quedará dividir el tamaño entre la capacidad de cada CD:

3788,8 / 700 = 5,4

El resultado es 5,4, es decir la película ocupará 5 CD´s completos y parte de otro por lo tanto necesitaremos 6 CD´s para grabar dicha película.

Problema tipo 2:

Se quieren almacenar en un disco duro de 500 GB todas las fotografías que sea posible, sabiendo que cada imagen ocupa 3600 KB. ¿Cuántas fotografías podremos almacenar en dicho disco duro?

Al igual que en el problema anterior, debemos dejar la misma unidad de medida en todas las cantidades, para ello pasaremos la unidad más grande a la más pequeña. En este caso para pasar de GB a KB, deberemos bajar dos peldaños de la escalera, multiplicando dos veces por 1024:

500 GB = 500 x 1024 x 1024= 524.288.000 KB

Bien ya tenemos la capacidad del disco duro expresada en KB, ahora nos queda dividir dicha cantidad entre el tamaño que ocupa cada imagen para obtener el número de fotografías que entrarán en dicho disco:

524.288.000 / 3600 =145635,55

Por lo tanto se podrán almacenar 145635 fotografías, observa que nos hemos quedado sólo con la parte entera del resultado.

 

Al igual que existen unidades de medida para la cantidad de información, también existen otras unidades que permiten medir la velocidad con la que ésta se transmite por las redes o Internet. Esas medidas son el bps (cantidad de bits por segundo) y B/s (Bytes por segundo) y sus correspondientes múltiplos (kbps, mbps, gbps, KB/s, MB/s y GB/s).  La gráfica de conversión entre unas y otras medidas se reflejan en el siguiente esquema:

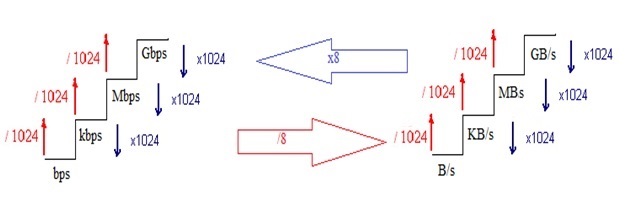
Escaleras de conversión entre diferentes unidades de medida de la velocidad de la información (Fuente: Elaboración propia)

 

Las unidades múltiplos del bps se suelen usar para medir las velocidades de las redes de información (por ejemplo la velocidad de una conexión ADSL se mide en Mbps) mientras que las unidades múltiplos del B/s las usan los programas de descarga como Torrent para medir la velocidad con la que se está descargando un archivo (normalmente la miden en KB/s).

Veamos otro problema tipo de la vida real en la que necesitemos utilizar las unidades de medida de la velocidad de la información:

Problema tipo 3:

Sabiendo que tenemos en casa una conexión ADSL de Internet de 10 mbps, contesta a la siguientes preguntas:

a) ¿Cúal es la velocidad en MB/s?

b) ¿Cuánto tiempo tardará  teóricamente en descargar una película de 1,3 GB?

c) ¿Cúantos MB se habrán descargado en 1 hora?

 

a) Lo que nos pide este apartado es que hagamos una conversión de mbps a MB/s, es decir cruzar al escalón de enfrente de la escalera de la derecha, para ello habrá que dividir la cantidad entre 8:

10 mbps = 10 /8 = 1,25 MB/s

b) Como el tamaño de la película se da en GB y la velocidad la acabamos de calcular en MB/s, tendremos que pasar los 1,3 GB que ocupa a MB multiplicando por 1024:

1,3 GB = 1,3 x 1024 = 1331,2 MB

El siguiente paso será dividir el tamaño de la película entre 1,25 que es la velocidad de nuestra línea, obteniendo así el número de segundos que tardará en descargarla:

1331,2 / 1,25 = 1064,96 segundos

El resultado es 1064,96 segundos, aproximadamente  unos 18 minutos.

c) El último apartado nos pide calcular el número de MB que podremos descargar con esa conexión a Internet en una hora. Si en un segundo hemos calculado que se descargan 1,25 MB en una hora se obtendrá multiplicando esa velocidad por 3600 segundos que tiene una hora:

1,25 x 3600 =  4500 MB